目标越大且距离越近，便越快到达，并比到达更小的更远的目标出错几率更低。此定律由保罗·莫里斯·菲茨（Paul Morris Fitts）提出，在人机交互和设计领域影响深远。运用此定律可以估算用户移动点击目标时所需的时间。
来源与推导过程
该定律由保罗·莫里斯·菲茨（Paul Morris Fitts）于 1954 年提出，他要求对象准确地在两个金属板之间来回敲打触控笔，并记录这一过程所用时间。通过不断改变两块金属板之间的距离和金属板宽度，最后得出公式：T = a + bLog2(D/W+1)，T = 移动设备所需时长；a、b 是经验常量，D = 设备起始位置和目标位置的距离；W = 目标的宽度大小。他认为，目的地明确的移动可以细分为两个部分：首先一个大幅度的移动将光标移向与目标大致相同的方向和区域；紧接着是一系列精细的小幅度微调来将光标精确定位在目标中心。

边界与限制

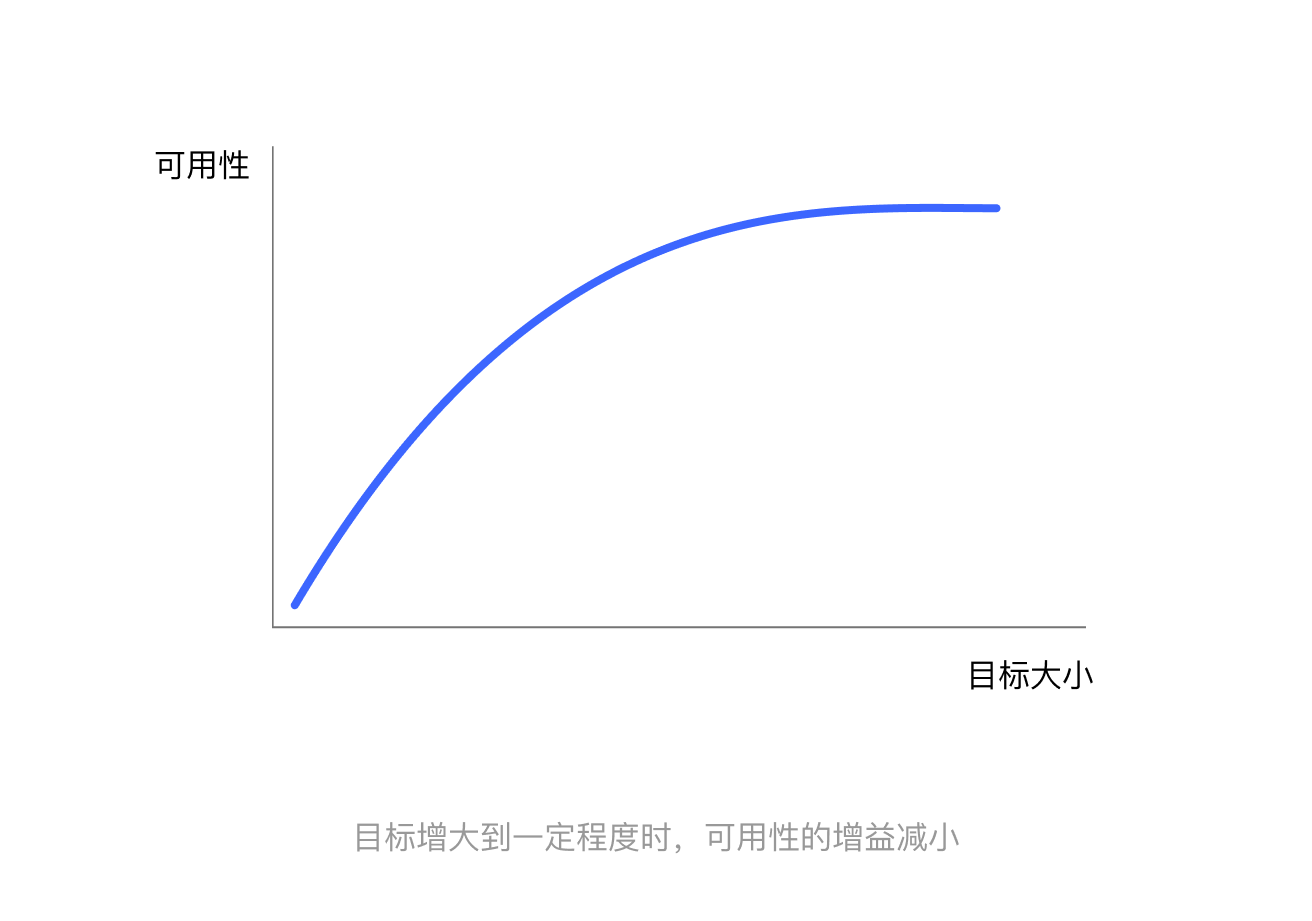
由于菲茨定律是一个对数函数而不是线性函数，随着目标的增大，可用性并不是呈线性增加。当目标足够大时，再增加尺寸得到的可用性增益很小。